AM 解调器

从调制波中提取原始消息信号的过程称为检测或解调。解调调制波的电路称为解调器。以下解调器（检测器）用于解调 AM 波。

• 平方律解调器
• 包络检测器

平方律解调器

平方律解调器用于解调低电平 AM 波。以下是平方律解调器的框图。

该解调器包含一个平方律设备和低通滤波器。 AM 波 $V_1left ( t ight )$ 作为该解调器的输入。

AM 波的标准形式为

$$V_1left ( t ight )=A_cleft [ 1+k_amleft ( t ight ) ight ] cosleft ( 2 pi f_ct ight )$$

我们知道平方律装置的输入和输出之间的数学关系为

$V_2left ( t ight )=k_1V_1left ( t ight )+k_2V_1^2left ( t ight )$(公式1)

其中，

$V_1left ( t ight )$ 是平方律装置的输入，它只是 AM 波

$V_2left ( t ight )$ 是平方律装置的输出

$k_1$ 和 $k_2$ 是常数

将 $V_1left ( t ight )$ 代入公式 1

$$V_2left ( t ight )=k_1left ( A_cleft [ 1+k_amleft ( t ight ) ight ] cosleft ( 2 pi f_ct ight ) ight )+k_2left ( A_cleft [ 1+k_amleft ( t ight ) ight ] cosleft ( 2 pi f_ct ight ) ight )^2$$

$Rightarrow V_2left ( t ight )=k_1A_c cos left ( 2 pi f_ct ight )+k_1A_ck_amleft ( t ight ) cos left ( 2 pi f_ct ight )+$

$k_2{A_{c}}^{2}left [ 1+{K_{a}}^{2}m^2left ( t ight )+2k_amleft ( t ight ) ight ]left ( ffrac{1+ cosleft ( 4 pi f_ct ight )}{2} ight )$

$Rightarrow V_2left ( t ight )=k_1A_c cos left ( 2 pi f_ct ight )+k_1A_ck_amleft ( t ight ) cos left ( 2 pi f_ct ight)+ffrac{K_2{A_{c}}^{2}}{2}+$

$ffrac{K_2{A_{c}}^{2}}{2} cos left ( 4 pi f_ct ight )+ffrac{k_2 {A_{c}}^{2}{k_{a}}^{2}m^2left ( t ight )}{2}+ffrac{k_2 {A_{c}}^{2}{k_{a}}^{2}m^2left ( t ight )}{2} cosleft ( 4 pi f_ct ight )+$

$k_2{A_{c}}^{2}k_amleft ( t ight )+k_2{A_{c}}^{2}k_amleft ( t ight )cos left ( 4 pi f_ct ight )$

在上面的等式中，项 $k_2{A_{c}}^{2}k_amleft ( t ight )$ 是消息信号的缩放版本。可以通过将上述信号通过低通滤波器来提取它，并借助耦合电容器消除直流分量$ffrac{k_2{A_{c}}^{2}}{2}$。

包络检波器

包络检波器用于检测（解调）高电平 AM 波。以下是包络检波器的框图。

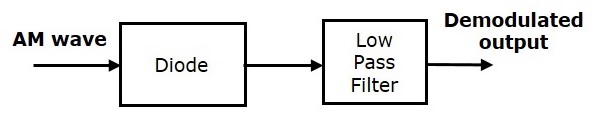
该包络检波器由二极管和低通滤波器组成。这里，二极管是主要检测元件。因此，包络检波器也称为二极管检波器。低通滤波器包含电阻和电容的并联组合。

AM 波 $sleft ( t ight )$ 作为此检测器的输入。

我们知道 AM 波的标准形式是

$$sleft ( t ight )=A_cleft [ 1+k_amleft ( t ight ) ight ] cosleft ( 2 pi f_ct ight )$$

在 AM 波的正半周期，二极管导通，电容充电至 AM 波的峰值。当 AM 波的值小于此值时，二极管将反向偏置。因此，电容将通过电阻 R 放电，直到下一个 AM 波的正半周期。当调幅波的值大于电容电压时，二极管导通，这个过程会重复。

我们应该这样选择元件值，使电容充电非常快，放电非常慢。这样，我们将得到与调幅波包络相同的电容电压波形，这几乎与调制信号相似。