角度调制
连续波调制中的另一种调制类型是角度调制。角度调制是载波信号的频率或相位根据消息信号而变化的过程。
角度调制波的标准方程是
$$sleft ( t ight )=A_c cos heta _ileft ( t ight )$$
其中,
$A_c$是调制波的幅度,与载波信号的幅度相同
$ heta _ileft ( t ight )$是调制波的角度
角度调制又分为频率调制和相位调制。
频率调制是载波信号的频率随消息信号线性变化的过程。
相位调制是载波信号的频率随消息信号线性变化的过程。
载波信号的相位与消息信号线性相关。
现在,让我们详细讨论一下。
频率调制
在幅度调制中,载波信号的幅度会发生变化。而在频率调制 (FM)中,载波信号的频率会根据调制信号的瞬时幅度而变化。
因此,在频率调制中,载波信号的幅度和相位保持不变。通过观察以下图表可以更好地理解这一点。
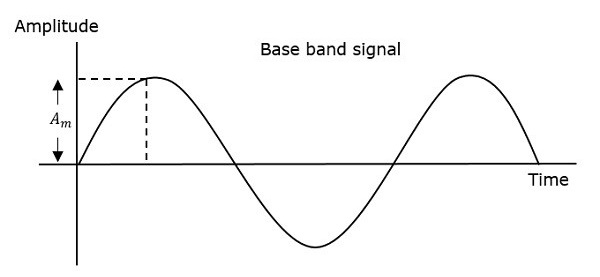
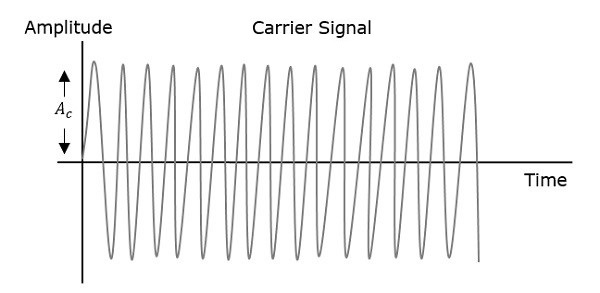
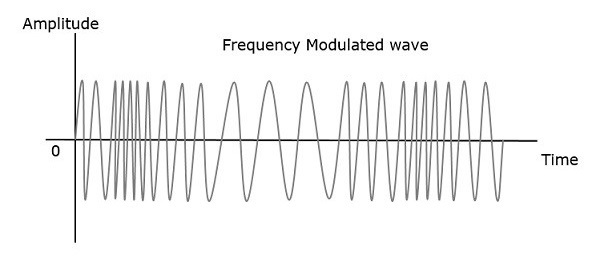
当调制或消息信号的幅度增加时,调制波的频率会增加。同样,当调制信号的幅度减小时,调制波的频率会降低。注意,当调制信号的幅度为零时,调制波的频率保持不变,等于载波信号的频率。
数学表示
FM调制中瞬时频率$f_i$的公式为
$$f_i=f_c+k_fmleft ( t ight )$$
其中,
$f_c$是载波频率
$k_t$是频率灵敏度
$mleft ( t ight )$是消息信号
我们知道角频率$omega_i$和角度$heta_ileft ( t ight )$之间的关系为
$$omega_i=ffrac{dheta_ileft ( t ight )}{dt}$$
$Rightarrow 2 pi f_i=ffrac{d heta _ileft ( t ight )}{dt}$
$Rightarrow heta _ileft ( t ight )= 2piint f_i dt$
将 $f_i$ 值代入上述等式中。
$$ heta _ileft ( t ight )=2 piint left ( f_c+k_f mleft ( t ight ) ight )dt$$
$Rightarrow heta _ileft ( t ight )=2 pi f_ct+2 pi k_fint mleft ( t ight )dt$
将 $ heta _ileft ( t ight )$ 值代入角度调制波的标准方程中。
$$sleft ( t ight )=A_c cosleft ( 2 pi f_ct + 2 pi k_f int mleft ( t ight )dt ight )$$
这是FM波的方程。
如果调制信号为 $mleft ( t ight )= A_m cos left ( 2 pi f_mt ight )$,则FM波的方程为
$$sleft ( t ight )=A_c cosleft ( 2 pi f_ct + \beta sin left ( 2 pi f_mt ight ) ight )$$
其中,
$\beta$ = 调制指数 $=ffrac{Delta f}{f_m}=ffrac{k_fA_m}{f_m}$
FM 调制频率(瞬时频率)与正常载波频率之间的差异称为频率偏差。它用 $Delta f$ 表示,等于 $k_f$ 和 $A_m$ 的乘积。
根据调制指数 $\beta$ 的值,FM 可分为窄带 FM和宽带 FM。
窄带 FM
窄带 FM 的特点如下。
与宽带 FM 相比,这种频率调制的带宽较小。
调制指数 $\beta$ 较小,即小于 1。
其频谱由载波、上边带和下边带组成。
用于移动通信,如警用无线、救护车、出租车等。
宽带 FM
宽带 FM 的特点如下。
这种频率调制具有无限带宽。
调制指数 $\beta$ 较大,即高于1.
其频谱由载波和位于其周围的无数边带组成。
这用于娱乐、广播应用,如调频广播、电视等。
相位调制
在频率调制中,载波的频率会发生变化。而在相位调制 (PM)中,载波信号的相位根据调制信号的瞬时幅度而变化。
因此,在相位调制中,载波信号的幅度和频率保持不变。通过观察以下图表可以更好地理解这一点。
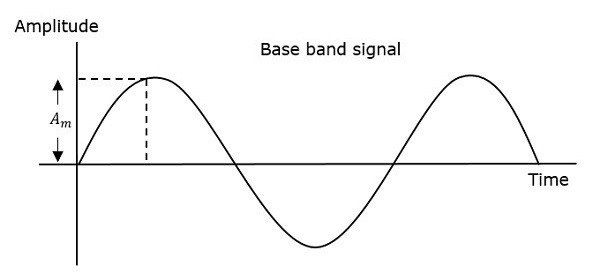
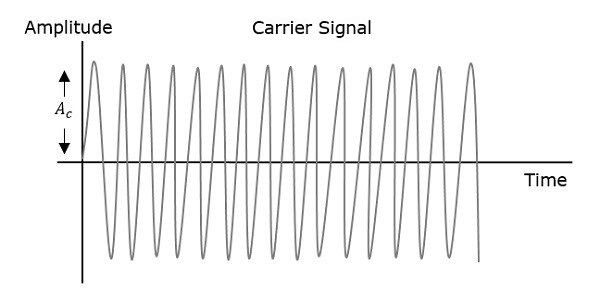
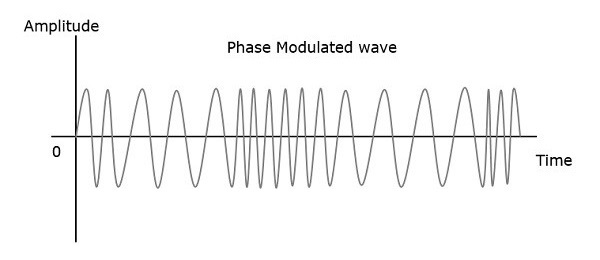
调制波的相位有无限多个点,波中的相移可能发生在这些点上。调制信号的瞬时幅度会改变载波信号的相位。当振幅为正时,相位向一个方向变化,如果振幅为负,相位向相反方向变化。
数学表示
相位调制中瞬时相位$phi_i$的方程为
$$phi _i=k_p mleft ( t ight )$$
其中,
$k_p$为相位灵敏度
$mleft ( t ight )$为信息信号
角度调制波的标准方程为
$$sleft ( t ight )=A_c cos left ( 2 pi f_ct+phi_i ight )$$
代入,上述方程中的 $phi_i$ 值。
$$sleft ( t ight )=A_c cos left ( 2 pi f_ct+k_p m left ( t ight ) ight )$$
这是PM 波的方程。
如果调制信号为 $mleft ( t ight )=A_m cos left ( 2 pi f_mt ight ) $,则 PM 波的方程为
$$sleft ( t ight )=A_c cosleft (2 pi f_ct+\beta cosleft ( 2 pi f_mt ight ) ight )$$
其中,
$\beta$ = 调制指数 = $Delta phi=k_pA_m$
$Delta phi$ 为相位偏差
相位调制用于移动通信系统,而频率调制主要用于调频广播。