SciPy 空间数据

---

使用空间数据

空间数据是指以几何空间表示的数据。

例如 坐标系上的点。

我们在许多任务中处理空间数据问题。

例如 判断一个点是否在边界内。

SciPy 为我们提供了模块 scipy.spatial，它具有处理空间数据的功能。

---

三角测量

多边形的三角剖分是将多边形分成多个三角形，我们可以用这些三角形计算多边形的面积。

带点的三角剖分意味着创建表面组成的三角形，其中所有给定的点都在表面中任何三角形的至少一个顶点上。

通过点生成这些三角剖分的一种方法是 Delaunay() 三角剖分。

实例

从以下点创建三角剖分:

import numpy as np
from scipy.spatial import Delaunay
import matplotlib.pyplot as plt

points = np.array([
  [2, 4],
  [3, 4],
  [3, 0],
  [2, 2],
  [4, 1]
])

simplices = Delaunay(points).simplices

plt.triplot(points[:, 0], points[:, 1], simplices)
plt.scatter(points[:, 0], points[:, 1], color='r')

plt.show()

结果:

亲自试一试 »

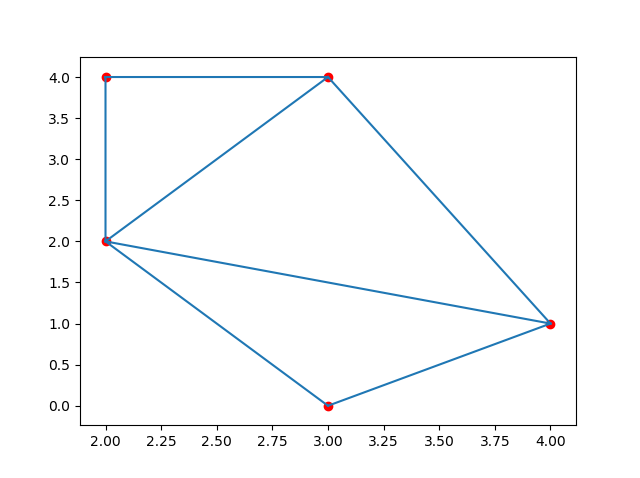
注释: The simplices property creates a generalization of the triangle notation.

---

凸包

凸包是覆盖所有给定点的最小多边形。

使用 ConvexHull() 方法创建一个 Convex Hull。

实例

为以下点创建一个凸包:

import numpy as np
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt

points = np.array([
  [2, 4],
  [3, 4],
  [3, 0],
  [2, 2],
  [4, 1],
  [1, 2],
  [5, 0],
  [3, 1],
  [1, 2],
  [0, 2]
])

hull = ConvexHull(points)
hull_points = hull.simplices

plt.scatter(points[:,0], points[:,1])
for simplex in hull_points:
  plt.plot(points[simplex,0], points[simplex,1], 'k-')

plt.show()

结果:

亲自试一试 »

---

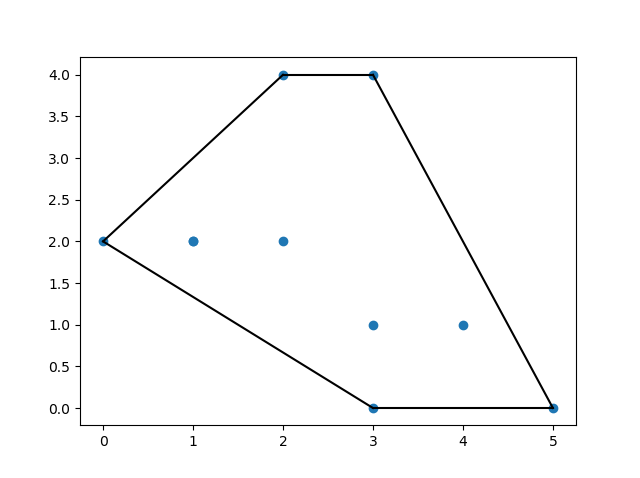
KDTrees

KDTrees 是一种针对最近邻查询优化的数据结构。

例如 在使用 KDTrees 的一组点中，我们可以有效地询问哪些点最接近某个给定点。

KDTree() 方法返回一个 KDTree 对象。

query() 方法返回到最近邻居的距离和邻居的位置。

实例

找到点 (1,1) 的最近邻:

from scipy.spatial import KDTree

points = [(1, -1), (2, 3), (-2, 3), (2, -3)]

kdtree = KDTree(points)

res = kdtree.query((1, 1))

print(res)

结果:

 (2.0, 0)

亲自试一试 »

---

距离矩阵

在数据科学中，有许多距离度量用于查找两点之间的各种类型的距离、欧几里得距离、余弦距离等。

两个向量之间的距离不仅可以是它们之间的直线长度，还可以是它们与原点的夹角，或者所需的单位步数等。

许多机器学习算法的性能很大程度上取决于距离度量。例如 "K 最近邻"或"K 均值"等。

让我们看一些距离度量:

---

欧式距离

求给定点之间的欧式距离。

实例

from scipy.spatial.distance import euclidean

p1 = (1, 0)
p2 = (10, 2)

res = euclidean(p1, p2)

print(res)

结果:

 9.21954445729

亲自试一试 »

---

城市街区距离（曼哈顿距离）

是使用 4 度运动计算的距离。

例如 我们只能移动:上、下、右或左，不能沿对角线移动。

实例

查找给定点之间的城市街区距离:

from scipy.spatial.distance import cityblock

p1 = (1, 0)
p2 = (10, 2)

res = cityblock(p1, p2)

print(res)

结果:

 11

亲自试一试 »

---

余弦距离

是A和B两点之间的余弦角值。

实例

求给定点之间的余弦距离:

from scipy.spatial.distance import cosine

p1 = (1, 0)
p2 = (10, 2)

res = cosine(p1, p2)

print(res)

结果:

 0.019419324309079777

亲自试一试 »

---

汉明距离

是两个位不同的位的比例。

这是一种测量二进制序列距离的方法。

实例

求给定点之间的汉明距离:

from scipy.spatial.distance import hamming

p1 = (True, False, True)
p2 = (False, True, True)

res = hamming(p1, p2)

print(res)

结果:

 0.666666666667

亲自试一试 »

---