控制系统 - 补偿器

补偿器有三种类型 - 滞后、超前和滞后-超前补偿器。这些是最常用的。

滞后补偿器

滞后补偿器是一种电气网络，当施加正弦输入时，它会生成具有相位滞后的正弦输出。下图显示了"s"域中的滞后补偿器电路。

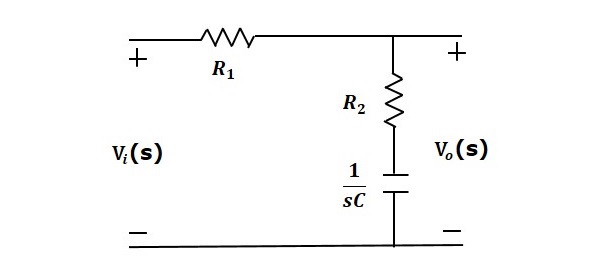
此处，电容器与电阻器 $R_2$ 串联，输出通过此组合进行测量。

此滞后补偿器的传递函数为 -

$$ffrac{V_o(s)}{V_i(s)}=ffrac{1}{alpha} left( ffrac{s+ffrac{1}{ au}}{s+ffrac{1}{alpha au}} ight )$$

其中，

$$ au=R_2C$$

$$alpha=ffrac{R_1+R_2}{R_2}$$

从上面的方程中，$alpha$ 总是大于 1。

从传递函数中，我们可以得出结论，滞后补偿器在 $s = − ffrac{1}{alpha au}$ 处有一个极点，在 $s = −ffrac{1}{ au}$ 处有一个零点。这意味着，在滞后补偿器的极点-零点配置中，极点将更接近原点。

代入传递函数中的$s = jomega$。

$$ffrac{V_o(jomega)}{V_i(jomega)}=ffrac{1}{alpha}left( ffrac{jomega+ffrac{1}{ au}}{jomega+ffrac{1}{alpha au}} ight )$$

相位角 $phi = an^{−1} omega au − tan^{−1} alphaomega au$

我们知道，输出正弦信号的相位等于输入正弦信号的相位角与传递函数的相位角之和。

因此，为了在该补偿器的输出端产生相位滞后，传递函数的相位角应该为负。当 $alpha > 时就会发生这种情况1$。

超前补偿器

超前补偿器是一种电网络，当施加正弦输入时，它会产生具有相位超前的正弦输出。下图显示了"s"域中的超前补偿器电路。

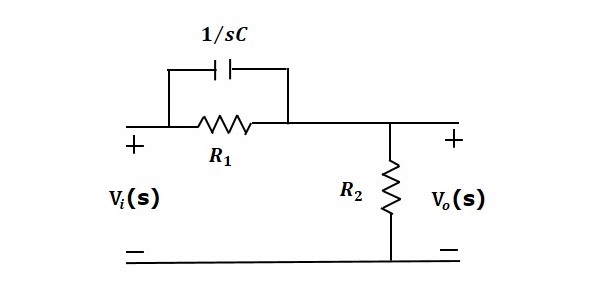
此处，电容器与电阻器 $R_1$ 并联，输出在电阻器 $R_2 上测量。

此超前补偿器的传递函数为 -

$$ffrac{V_o(s)}{V_i(s)}=\beta left( ffrac{s au+1}{\beta s au+1} ight )$$

其中，

$$ au=R_1C$$

$$\beta=ffrac{R_2}{R_1+R_2}$$

从传递函数中，我们可以得出结论，超前补偿器极点在 $s = −ffrac{1}{\beta}$，零点在 $s = − ffrac{1}{\beta au}$。

代入传递函数中的 $s = jomega$。

$$ffrac{V_o(jomega)}{V_i(jomega)}=\beta left( ffrac{jomega au+1}{\beta j omega au+1} ight )$$

相位角 $phi = tan^{−1}omega au − tan^{−1}\betaomega au$

我们知道，输出正弦信号的相位等于输入正弦信号的相位角与传递函数之和。

因此，为了在该补偿器的输出端产生相位超前，相位传递函数的角度应为正。当 $0 < \beta < 1$ 时，就会发生这种情况。因此，在超前补偿器的极点零配置中，零点将更接近原点。

滞后超前补偿器

滞后超前补偿器是一个电气网络，它在一个频率区域产生相位滞后，在另一个频率区域产生相位超前。它是滞后和超前补偿器的组合。下图显示了"s"域中的滞后超前补偿器电路。

该电路看起来像两个补偿器都是级联的。因此，该电路的传递函数将是超前和滞后补偿器传递函数的乘积。

$$ffrac{V_o(s)}{V_i(s)}=\beta left( ffrac{s au_1+1}{\beta s au_1+1} ight )ffrac{1}{alpha} left ( ffrac{s+ffrac{1}{ au_2}}{s+ffrac{1}{alpha au_2}} ight )$$

我们知道 $alpha\beta=1$。

$$Rightarrow ffrac{V_o(s)}{V_i(s)}=left ( ffrac{s+ffrac{1}{ au_1}}{s+ffrac{1}{\beta au_1}} ight )left ( ffrac{s+ffrac{1}{ au_2}}{s+ffrac{1}{alpha au_2}} ight )$$

其中，

$$ au_1=R_1C_1$$

$$ au_2=R_2C_2$$