一阶系统的响应
在本章中,我们来讨论一阶系统的时间响应。考虑以下闭环控制系统的框图。这里,开环传递函数 $ffrac{1}{sT}$ 与一个单位负反馈相连。
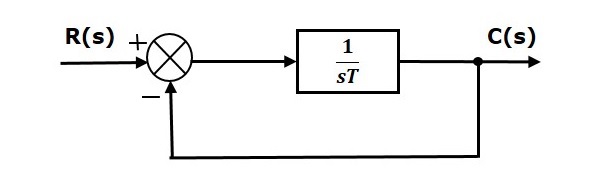
我们知道,闭环控制系统的传递函数具有单位负反馈,因为,
$$ffrac{C(s)}{R(s)}=ffrac{G(s)}{1+G(s)}$$
代入上式中的 $G(s)=ffrac{1}{sT}$。
$$ffrac{C(s)}{R(s)}=ffrac{ffrac{1}{sT}}{1+ffrac{1}{sT}}=ffrac{1}{sT+1}$$
s 的幂是分母中的 1 学期。 因此,上述传递函数是一阶的,系统被称为一阶系统。
我们可以将上述方程重写为
$$C(s)=left ( ffrac{1}{sT+1} ight )R(s)$$
其中,
C(s)是输出信号 c(t) 的拉普拉斯变换,
R(s)是输入信号 r(t) 的拉普拉斯变换,
T是时间常数。
按照以下步骤获取时间域中一阶系统的响应(输出)。
对输入进行拉普拉斯变换信号 $r(t)$。
考虑方程 $C(s)=left ( ffrac{1}{sT+1} ight )R(s)$
将 $R(s)$ 值代入上述方程中。
如有必要,对 $C(s)$ 进行部分分式运算。
对 $C(s)$ 进行逆拉普拉斯变换。
在上一章中,我们已经看到了标准测试信号,如脉冲、阶跃、斜坡和抛物线。现在让我们逐一找出一阶系统对每个输入的响应。响应的名称根据输入信号的名称给出。例如,系统对脉冲输入的响应称为脉冲响应。
一阶系统的脉冲响应
将单位脉冲信号视为一阶系统的输入。
因此,$r(t)=delta (t)$
对两边应用拉普拉斯变换。
$R(s)=1$
考虑方程,$C(s)=left ( ffrac{1}{sT+1} ight )R(s)$
在上述方程中代入 $R(s) = 1$。
$$C(s)=left ( ffrac{1}{sT+1} ight )(1)=ffrac{1}{sT+1}$$
将上述方程重新排列为拉普拉斯变换的标准形式之一。
$$C(s)=ffrac{1}{Tleft ( s+ffrac{1}{T} ight )} Rightarrow C(s)=ffrac{1}{T}left ( ffrac{1}{s+ffrac{1}{T}} ight )$$
对两边应用逆拉普拉斯变换。
$$c(t)=ffrac{1}{T}e^left ( {-ffrac{t}{T}} ight )u(t)$$
单位脉冲响应如下图所示。
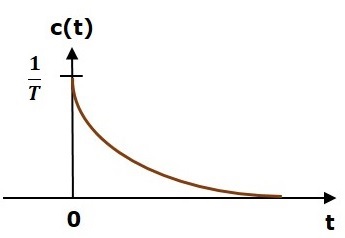
单位脉冲响应,c(t) 是"t"为正值的指数衰减信号,而"t"为负值的则为零。
一阶系统的阶跃响应
将单位阶跃信号视为一阶系统的输入。
So, $r(t)=u(t)$
对两边应用拉普拉斯变换。
$$R(s)=ffrac{1}{s}$$
考虑方程 $C(s)=left ( ffrac{1}{sT+1} ight )R(s)$
将 $R(s)=ffrac{1}{s}$ 代入上述方程中。
$$C(s)=left ( ffrac{1}{sT+1} ight )left ( ffrac{1}{s} ight )=ffrac{1}{sleft ( sT+1 ight )}$$
对 C(s) 进行部分分式。
$$C(s)=ffrac{1}{sleft ( sT+1 ight )}=ffrac{A}{s}+ffrac{B}{sT+1}$$
$$Rightarrow ffrac{1}{sleft ( sT+1 ight )}=ffrac{Aleft ( sT+1 ight )+Bs}{sleft ( sT+1 ight )}$$
两边的分母项相同。因此,它们会相互抵消。因此,使分子项相等。
$$1=Aleft ( sT+1 ight )+Bs$$
通过使两边的常数项相等,您将得到 A = 1。
代入 A = 1 并让两边的 s 项的系数相等。
$$0=T+B Rightarrow B=-T$$
代入 $C(s)$ 的部分分式展开式中的 A = 1 和 B = −T。
$$C(s)=ffrac{1}{s}-ffrac{T}{sT+1}=ffrac{1}{s}-ffrac{T}{Tleft ( s+ffrac{1}{T} ight )}$$
$$Rightarrow C(s)=ffrac{1}{s}-ffrac{1}{s+ffrac{1}{T}}$$
对两边应用逆拉普拉斯变换。
$$c(t)=left ( 1-e^{-left ( ffrac{t}{T} ight )} ight )u(t)$$
单位阶跃响应,c(t) 具有瞬态和稳态项。
单位阶跃响应中的瞬态项为 -
$$c_{tr}(t)=-e^{-left ( ffrac{t}{T} ight )}u(t)$$
单位阶跃响应中的稳态项为 -
$$c_{ss}(t)=u(t)$$
下图显示了单位阶跃响应。
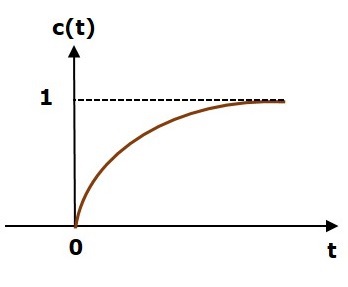
单位阶跃响应 c(t) 的值在 t = 0 时为零,并且对于所有 t 负值也是如此。它从零值逐渐增加,最终在稳定状态下达到 1。因此,稳态值取决于输入的大小。
一阶系统的斜坡响应
将单位斜坡信号视为一阶系统的输入。
$因此,r(t)=tu(t)$
对两边应用拉普拉斯变换。
$$R(s)=ffrac{1}{s^2}$$
考虑方程,$C(s)=left ( ffrac{1}{sT+1} ight )R(s)$
在上述方程中代入 $R(s)=ffrac{1}{s^2}$。
$$C(s)=left ( ffrac{1}{sT+1} ight )left ( ffrac{1}{s^2} ight )=ffrac{1}{s^2(sT+1)}$$
对 $C(s)$ 进行部分分式计算。
$$C(s)=ffrac{1}{s^2(sT+1)}=ffrac{A}{s^2}+ffrac{B}{s}+ffrac{C}{sT+1}$$
$$Rightarrow ffrac{1}{s^2(sT+1)}=ffrac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$
两边的分母项相同。因此,它们会相互抵消。因此,使分子项相等。
$$1=A(sT+1)+Bs(sT+1)+Cs^2$$
通过使两边的常数项相等,您将得到 A = 1。
代入 A = 1 并让两边的 s 项的系数相等。
$$0=T+B Rightarrow B=-T$$
类似地,代入 B = −T 并让两边的 $s^2$ 项的系数相等。您将得到 $C=T^2$。
在 $C(s)$ 的部分分式展开式中代入 A = 1、B = −T 和 $C = T^2$。
$$C(s)=ffrac{1}{s^2}-ffrac{T}{s}+ffrac{T^2}{sT+1}=ffrac{1}{s^2}-ffrac{T}{s}+ffrac{T^2}{Tleft ( s+ffrac{1}{T} ight )}$$
$$Rightarrow C(s)=ffrac{1}{s^2}-ffrac{T}{s}+ffrac{T}{s+ffrac{1}{T}}$$
对两边应用逆拉普拉斯变换。
$$c(t)=left ( t-T+Te^{-left ( ffrac{t}{T} ight )} ight )u(t)$$
单位斜坡响应,c(t) 具有瞬态和稳态项。
单位斜坡响应中的瞬态项为 -
$$c_{tr}(t)=Te^{-left ( ffrac{t}{T} ight )}u(t)$$
单位斜坡响应中的稳态项为 -
$$c_{ss}(t)=(t-T)u(t)$$
下图显示了单位斜坡响应。

单位斜坡响应,c(t) 对于 t 的所有正值都遵循单位斜坡输入信号。但是,与输入信号存在 T 个单位的偏差。
一阶系统的抛物线响应
将单位抛物线信号视为一阶系统的输入。
因此,$r(t)=ffrac{t^2}{2}u(t)$
对两边应用拉普拉斯变换。
$$R(s)=ffrac{1}{s^3}$$
考虑方程,$C(s)=left ( ffrac{1}{sT+1} ight )R(s)$
将 $R(s)=ffrac{1}{s^3}$ 代入上述方程。
$$C(s)=left ( ffrac{1}{sT+1} ight )left( ffrac{1}{s^3} ight )=ffrac{1}{s^3(sT+1)}$$
对$C(s)$进行部分分式化简。
$$C(s)=ffrac{1}{s^3(sT+1)}=ffrac{A}{s^3}+ffrac{B}{s^2}+ffrac{C}{s}+ffrac{D}{sT+1}$$
化简后,A、B、C、D的值分别为1、$-T、: T^2:、: −T^3$。将这些值代入上述 C(s) 的部分分式展开式中。
$C(s)=ffrac{1}{s^3}-ffrac{T}{s^2}+ffrac{T^2}{s}-ffrac{T^3}{sT+1} : Rightarrow C(s)=ffrac{1}{s^3}-ffrac{T}{s^2}+ffrac{T^2}{s}-ffrac{T^2}{s+ffrac{1}{T}}$
对两边应用逆拉普拉斯变换。
$$c(t)=left ( ffrac{t^2}{2} -Tt+T^2-T^2e^{-left ( ffrac{t}{T} ight )} ight )u(t)$$
单位抛物线响应,c(t) 既有瞬态项也有稳态项。
单位抛物线响应中的瞬态项是
$$C_{tr}(t)=-T^2e^{-left ( ffrac{t}{T} ight )}u(t)$$
单位抛物线响应中的稳态项是
$$C_{ss}(t)=left ( ffrac{t^2}{2} -Tt+T^2 ight )u(t)$$
从这些响应中,我们可以得出结论,一阶控制系统在斜坡和抛物线输入下不稳定,因为这些响应即使在无限长的时间内也会不断增加。一阶控制系统在脉冲和阶跃输入下是稳定的,因为这些响应具有有界输出。但是,脉冲响应没有稳态项。因此,阶跃信号在时间域中被广泛用于根据其响应来分析控制系统。