二阶系统的响应

本章将讨论二阶系统的时间响应。考虑以下闭环控制系统的框图。这里，开环传递函数 $ffrac{omega ^2_n}{s(s+2delta omega_n)}$ 与一个单位负反馈相连。

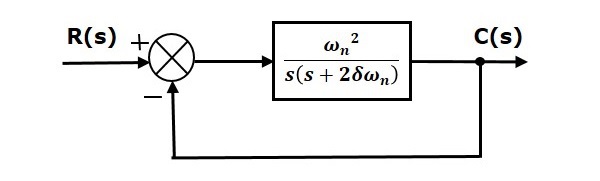
我们知道，具有单位负反馈的闭环控制系统的传递函数为

$$ffrac{C(s)}{R(s)}=ffrac{G(s)}{1+G(s)}$$

将 $G(s)=ffrac{omega ^2_n}{s(s+2delta omega_n)}$ 代入上式。

$$ffrac{C(s)}{R(s)}=ffrac{left (ffrac{omega ^2_n}{s(s+2delta omega_n)} ight )}{1+ left ( ffrac{omega ^2_n}{s(s+2delta omega_n)} ight )}=ffrac{omega _n^2}{s^2+2delta omega _ns+omega _n^2}$$

分母项中's'的幂为2。因此，上述传递函数是二阶的，系统被称为二阶系统。

特征方程为 -

$$s^2+2delta omega _ns+omega _n^2=0$$

特征方程的根为 -

$$s=ffrac{-2omega delta _npm sqrt{(2deltaomega _n)^2-4omega _n^2}}{2}=ffrac{-2(deltaomega _npm omega _nsqrt{delta ^2-1})}{2}$$

$$Rightarrow s=-delta omega_n pm omega _nsqrt{delta ^2-1}$$

• 当 δ = 0 时，两个根为虚数。
• 当 δ = 1 时，两个根为实数且相等。
• 当 δ > 1 时，两个根为实数但不相等。
• 当 0 < δ < 时，两个根为复共轭1.

我们可以将 $C(s)$ 方程写为，

$$C(s)=left ( ffrac{omega _n^2}{s^2+2deltaomega_ns+omega_n^2} ight )R(s)$$

其中，

• C(s) 是输出信号的拉普拉斯变换，c(t)

• R(s) 是输入信号的拉普拉斯变换，r(t)

• ω_n 是固有频率

• δ 是阻尼比。

按照以下步骤获取响应（输出）在时间域中的二阶系统。

• 对输入信号 $r(t)$ 进行拉普拉斯变换。

• 考虑方程 $C(s)=left ( ffrac{omega _n^2}{s^2+2deltaomega_ns+omega_n^2} ight )R(s)$

• 将 $R(s)$ 值代入上述方程中。

• 如果需要，对 $C(s)$ 进行部分分式。

• 对 $C(s)$ 进行逆拉普拉斯变换。

二阶系统的阶跃响应

将单位阶跃信号视为二阶系统的输入。

单位阶跃信号的拉普拉斯变换阶跃信号为，

$$R(s)=ffrac{1}{s}$$

我们知道二阶闭环控制系统的传递函数为，

$$ffrac{C(s)}{R(s)}=ffrac{omega _n^2}{s^2+2deltaomega_ns+omega_n^2}$$

情况 1：δ = 0

代入传递函数中的 $delta = 0$。

$$ffrac{C(s)}{R(s)}=ffrac{omega_n^2}{s^2+omega_n^2}$$

$$Rightarrow C(s)=left( ffrac{omega_n^2}{s^2+omega_n^2} ight )R(s)$$

代入上述等式中的 $R(s) = ffrac{1}{s}$。

$$C(s)=left( ffrac{omega_n^2}{s^2+omega_n^2} ight )left( ffrac{1}{s} ight )=ffrac{omega_n^2}{s(s^2+omega_n^2)}$$

对两边应用逆拉普拉斯变换。

$$c(t)=left ( 1-cos(omega_n t) ight )u(t)$$

因此，当 $/delta = 0$ 时，二阶系统的单位阶跃响应将是具有恒定幅度和频率的连续时间信号。

案例 2：δ = 1

代入传递函数中的 $/delta = 1$。

$$ffrac{C(s)}{R(s)}=ffrac{omega_n^2}{s^2+2omega_ns+omega_n^2}$$

$$Rightarrow C(s)=left( ffrac{omega_n^2}{(s+omega_n)^2} ight)R(s)$$

代入上述等式中的 $R(s) = ffrac{1}{s}$。

$$C(s)=left( ffrac{omega_n^2}{(s+omega_n)^2} ight)left ( ffrac{1}{s} ight)=ffrac{omega_n^2}{s(s+omega_n)^2}$$

对 $C(s)$ 进行部分分式化。

$$C(s)=ffrac{omega_n^2}{s(s+omega_n)^2}=ffrac{A}{s}+ffrac{B}{s+omega_n}+ffrac{C}{(s+omega_n)^2}$$

化简后，A、B、C 的值分别为 $1,: -1: 和 : −omega _n$。将这些值代入上述 $C(s)$ 的部分分式展开式中。

$$C(s)=ffrac{1}{s}-ffrac{1}{s+omega_n}-ffrac{omega_n}{(s+omega_n)^2}$$

对两边应用逆拉普拉斯变换。

$$c(t)=(1-e^{-omega_nt}-omega _nte^{-omega_nt})u(t)$$

因此，二阶系统的单位阶跃响应将尝试在稳定状态下达到阶跃输入。

情况 3：0 < δ < 1

我们可以修改传递函数的分母项如下 −

$$s^2+2deltaomega_ns+omega_n^2=left { s^2+2(s)(delta omega_n)+(delta omega_n)^2 ight }+omega_n^2-(deltaomega_n)^2$$

$$=(s+deltaomega_n)^2+omega_n^2(1-delta^2)$$

传递函数变成，

$$ffrac{C(s)}{R(s)}=ffrac{omega_n^2}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)}$$

$$Rightarrow C(s)=left( ffrac{omega_n^2}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)} ight )R(s)$$

代入上述等式中的 $R(s) = ffrac{1}{s}$。

$$C(s)=left( ffrac{omega_n^2}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)} ight )left( ffrac{1}{s} ight )=ffrac{omega_n^2}{sleft ((s+deltaomega_n)^2+omega_n^2(1-delta^2) ight)}$$

对 $C(s)$ 进行部分分式化。

$$C(s)=ffrac{omega_n^2}{sleft ((s+deltaomega_n)^2+omega_n^2(1-delta^2) ight)}=ffrac{A}{s}+ffrac{Bs+C}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)}$$

化简后，A、B、C 的值分别为 $1,: -1 : 和 : −2delta omega _n$分别代入上述 C(s) 的部分分式展开式中的这些值。

$$C(s)=ffrac{1}{s}-ffrac{s+2deltaomega_n}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)}$$

$$C(s)=ffrac{1}{s}-ffrac{s+deltaomega_n}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)}-ffrac{deltaomega_n}{(s+deltaomega_n)^2+omega_n^2(1-delta^2)}$$

$C(s)=ffrac{1}{s}-ffrac{(s+deltaomega_n)}{(s+deltaomega_n)^2+(omega_nsqrt{1-delta^2})^2}-ffrac{delta}{sqrt{1-delta^2}}left ( ffrac{omega_nsqrt{1-delta^2}}{(s+deltaomega_n)^2+(omega_nsqrt{1-delta^2})^2} ight )$

将上面的 $omega_nsqrt{1-delta^2}$ 替换为 $omega_d$方程。

$$C(s)=ffrac{1}{s}-ffrac{(s+deltaomega_n)}{(s+deltaomega_n)^2+omega_d^2}-ffrac{delta}{sqrt{1-delta^2}}left ( ffrac{omega_d}{(s+deltaomega_n)^2+omega_d^2} ight )$$

对两边应用逆拉普拉斯变换。

$$c(t)=left ( 1-e^{-delta omega_nt}cos(omega_dt)-ffrac{delta}{sqrt{1-delta^2}}e^{-deltaomega_nt}sin(omega_dt) ight )u(t)$$

$$c(t)=left ( 1-ffrac{e^{-deltaomega_nt}}{sqrt{1-delta^2}}left ( (sqrt{1-delta^2})cos(omega_dt)+delta sin(omega_dt) ight ) ight )u(t)$$

如果 $sqrt{1-delta^2}=sin( heta)$，则'δ' 将是 cos(θ)。将这些值代入上述方程。

$$c(t)=left ( 1-ffrac{e^{-deltaomega_nt}}{sqrt{1-delta^2}}(sin( heta)cos(omega_dt)+cos( heta)sin(omega_dt)) ight )u(t)$$

$$Rightarrow c(t)=left ( 1-left ( ffrac{e^{-deltaomega_nt}}{sqrt{1-delta^2}} ight )sin(omega_dt+ heta) ight )u(t)$$

因此，当'δ'介于零和一之间时，二阶系统的单位阶跃响应具有阻尼振荡（幅度减小）。

案例4：δ > 1

我们可以修改传递函数的分母项，如下所示 −

$$s^2+2deltaomega_ns+omega_n^2=left { s^2+2(s)(deltaomega_n)+(deltaomega_n)^2 ight }+omega_n^2-(deltaomega_n)^2$$

$$=left ( s+deltaomega_n ight )^2-omega_n^2left ( delta^2-1 ight )$$

传递函数变为，

$$ffrac{C(s)}{R(s)}=ffrac{omega_n^2}{(s+deltaomega_n)^2-omega_n^2(delta^2-1)}$$

$$Rightarrow C(s)=left ( ffrac{omega_n^2}{(s+deltaomega_n)^2-omega_n^2(delta^2-1)} ight )R(s)$$

代入上述等式中的 $R(s) = ffrac{1}{s}$。

$C(s)=left ( ffrac{omega_n^2}{(s+deltaomega_n)^2-(omega_nsqrt{delta^2-1})^2} ight )left ( ffrac{1}{s} ight )=ffrac{omega_n^2}{s(s+deltaomega_n+omega_nsqrt{delta^2-1})(s+deltaomega_n-omega_nsqrt{delta^2-1})}$

对部分分式进行$C(s)$。

$$C(s)=ffrac{omega_n^2}{s(s+deltaomega_n+omega_nsqrt{delta^2-1})(s+deltaomega_n-omega_nsqrt{delta^2-1})}$$

$$=ffrac{A}{s}+ffrac{B}{s+deltaomega_n+omega_nsqrt{delta^2-1}}+ffrac{C}{s+deltaomega_n-omega_nsqrt{delta^2-1}}$$

化简后，A、B、C 的值分别为 1、$ffrac{1}{2(delta+sqrt{delta^2-1})(sqrt{delta^2-1})}$ 和分别为 $ffrac{-1}{2(delta-sqrt{delta^2-1})(sqrt{delta^2-1})}$。将这些值代入上述 $C(s)$ 的部分分式展开式中。

$$C(s)=ffrac{1}{s}+ffrac{1}{2(delta+sqrt{delta^2-1})(sqrt{delta^2-1})}left ( ffrac{1}{s+deltaomega_n+omega_nsqrt{delta^2-1}} ight )-left ( ffrac{1}{2(delta-sqrt{delta^2-1})(sqrt{delta^2-1})} ight )left ( ffrac{1}{s+deltaomega_n-omega_nsqrt{delta^2-1}} ight )$$

对两边应用逆拉普拉斯变换。

$c(t)=left ( 1+left ( ffrac{1}{2(delta+sqrt{delta^2-1})(sqrt{delta^2-1})} ight )e^{-(deltaomega_n+omega_nsqrt{delta^2-1})t}-left ( ffrac{1}{2(delta-sqrt{delta^2-1})(sqrt{delta^2-1})} ight )e^{-(deltaomega_n-omega_nsqrt{delta^2-1})t} ight )u(t)$

由于过阻尼，当 δ > 时，二阶系统的单位阶跃响应1 在稳定状态下永远不会达到阶跃输入。

二阶系统的脉冲响应

二阶系统的脉冲响应可以通过使用这两种方法中的任何一种来获得。

• 在推导阶跃响应时，请遵循所涉及的程序，将 $R(s)$ 的值视为 1 而不是 $ffrac{1}{s}$。

• 对阶跃响应进行微分。

下表显示了 4 种阻尼比情况下二阶系统的脉冲响应。