感应电动势的概念
根据电磁感应原理,当连接到导体或线圈的磁通量发生变化时,导体或线圈中就会感应出 EMF。在实践中,使用以下两种方法来改变磁通量。
方法 1 − 导体在静止磁场中移动
我们可以在静止磁场中移动导体或线圈,这样连接到导体或线圈的磁通量就会发生变化。因此,导体中就会感应出 EMF。这种感应 EMF 被称为动态感应 EMF。之所以这样称呼,是因为运动中的导体中会产生 EMF。动态感应 EMF 的例子是交流和直流发电机中产生的 EMF。
方法 2 −静止导体置于变化的磁场中
当静止导体或线圈置于移动或变化的磁场中时,导体或线圈中会产生 EMF。以这种方式产生的 EMF 称为静态感应 EMF。之所以这样称呼,是因为 EMF 是在静止的导体中产生的。变压器中感应出的 EMF 是静态感应 EMF 的一个例子。
因此,从讨论中可以清楚地看出,感应 EMF 可以分为两大类,即:
动态感应 EMF
静态感应 EMF
动态感应 EMF
如上一节所述,动态感应 EMF是在静止磁场中的移动导体或线圈中感应出的 EMF。动态感应 EMF 的表达式可推导出如下 −
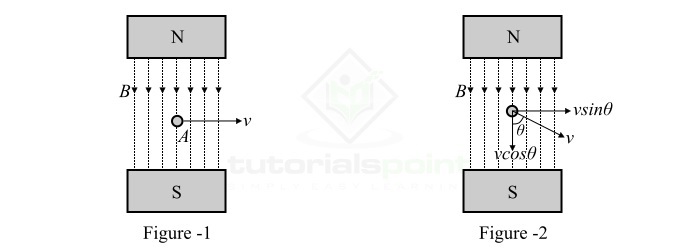
考虑一个长度为 l 米的单个导体,位于磁通密度为 B Wb/m2 的均匀磁场中,如图 1 所示。该导体以 v m/s 的速度相对于磁场以直角移动。
现在,如果导体在 dt 秒的时间内移动一小段距离 dx,则导体扫过的面积为,
$$mathrm{mathit{A:=:l imes dx:}mathrm{m^{mathrm{2}}}}$$
因此,导体切割的磁通量为,
$$mathrm{mathit{dphi }:=:mathrm{Flux:density imes Area: swept}}$$
$$mathrm{Rightarrow mathit{dphi }:=:mathit{B imes l imes dx}:mathrm{Wb}}$$
根据法拉第电磁感应定律,导体中感应出的 EMF 为:
$$mathrm{mathit{e}:=:mathit{N}ffrac{mathit{dphi }}{mathit{dt}}:=:mathit{N}ffrac{mathit{Bldx}}{mathit{dt}}}$$
由于我们只取单个导体,因此 N = 1。
$$mathrm{mathit{e}:=:mathit{Blv}:mathrm{volts}cdot cdot cdot (1)}$$
其中,v = dx/dt,导体在磁场中的速度。
如果导体在磁场中发生角运动,并且导体相对于磁场以角度 θ 移动,如图 2 所示。那么,导体穿过磁场的速度等于"vsinθ"。因此,感应 EMF 定义为,
$$mathrm{mathit{e}:=:mathit{B:l:v}:mathrm{sinmathit{ heta }}:mathrm{volts}cdot cdot cdot (2)}$$
静态感应 EMF
当将静止导体放置在变化的磁场中时,导体中感应出的 EMF 称为静态感应 EMF。静态感应 EMF 进一步分为以下两种类型 −
自感 EMF
互感 EMF
自感 EMF
当由于自身磁通链变化而在导体或线圈中感应出 EMF 时,它被称为自感 EMF。
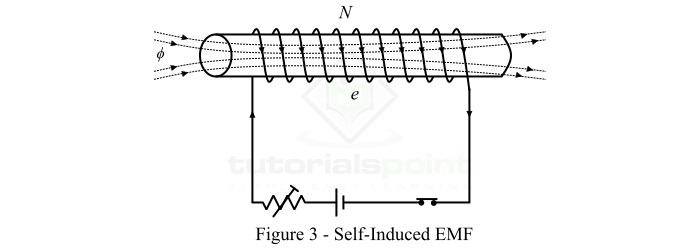
考虑一个 N 匝线圈,如图 3 所示。流过线圈的电流在线圈中建立磁场。如果线圈中的电流发生变化,则链接线圈的磁通量也会发生变化。根据法拉第电磁感应定律,这种变化的磁场会在线圈中感应出 EMF。这种 EMF 称为自感 EMF,其大小由下式给出:
$$mathrm{mathit{e}:=:mathit{N}ffrac{mathit{dphi }}{mathit{dt}}}$$
互感 EMF
由于相邻线圈的磁场变化而在线圈中感应出的 EMF 称为互感 EMF。
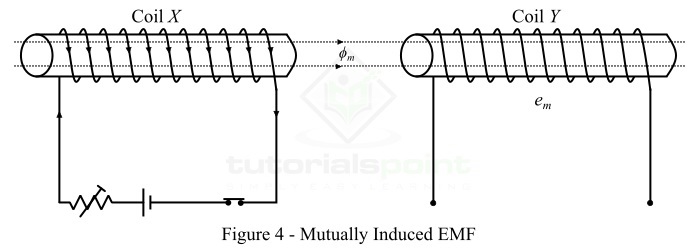
考虑两个彼此相邻放置的线圈 X 和 Y,如图 4 所示。这里,线圈 X 产生的磁通量的一部分与线圈 Y 相连。线圈 X 的磁通量是线圈 X 和 Y 共同的,被称为互通磁通 ($mathit{phi _{m}}$)。
如果线圈 X 中的电流发生变化,则互通磁通也会发生变化,因此两个线圈中都会产生 EMF。其中,线圈 X 中感应出的 EMF 称为自感 EMF,线圈 Y 中感应出的 EMF 称为互感 EMF。
根据法拉第定律,互感 EMF 的大小由下式给出:
$$mathrm{mathit{e_{m}}:=:mathit{N_{Y}}ffrac{mathit{dphi _{m}}}{mathit{dt}}}$$
其中,$mathit{N_{Y}}$ 为线圈 Y 的匝数,$ffrac{mathit{dphi _{m}}}{mathit{dt}}$ 为互感磁通的变化率。