直流电机的工作原理

直流电机的工作原理基于电磁相互作用定律。根据该定律，每当载流导体或线圈被放置在磁场中时，导体或线圈都会受到电磁力。

该力的大小由以下公式给出：

$$mathrm{mathit{F=BIL}}$$

其中，

• $mathit{B}$ 是磁通密度，

• $mathit{I}$ 是导体或线圈中流动的电流，

• $mathit{l}$ 是导体的长度。

该力的方向可以通过我们在本教程的模块 1（基本概念）中讨论过的弗莱明左手定则 (FLHR) 确定。

为了理解直流电机，考虑如图 1 所示的两极直流电机。

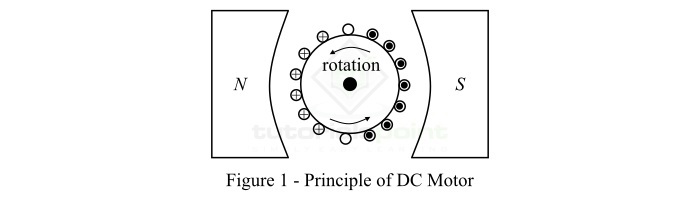
当此直流电机的端子连接到外部直流电源时，机器内部会发生以下两种现象 −

• 场电磁铁被激发，产生交替的 N 和 S 极。

• 电枢导体承载电流。其中，N 极下的导体在一个方向上承载电流（比如说在纸平面内），而 S 极下的导体在相反方向上承载电流（比如说在纸平面外）。

因为在这种情况下，每个导体都承载电流并放置在磁场中。由于电流和磁场的相互作用，机械力作用在导体上。

通过应用弗莱明左手定则，很明显，每个导体上的机械力都倾向于使导体沿逆时针方向移动。所有导体上的机械力加在一起产生驱动扭矩，使电枢旋转。

当导体从一个极侧移动到另一极时，由于换向作用，该导体中的电流会反转，同时受到下一个极性相反的极的影响。因此，导体上力的方向保持不变。这样，直流电动机的电枢就会连续朝一个方向旋转。

直流电动机的电枢转矩

直流电动机的电枢绕其轴线旋转。因此，作用在电枢上的机械力称为电枢转矩。它被定义为作用在电枢导体上的力的转矩，由下式给出：

$$mathrm{mathit{ au _{a}}/conductor:=:mathit{F imes r}}$$

其中，F是每个导体上的力，r是电枢的平均半径。

如果 Z 是电枢中的导体数量，则总电枢扭矩由下式给出：

$$mathrm{ 因此 mathit{ au _{a}}:=:mathit{ZF imes r}:=:mathit{ZBIL imes r}}$$

因为，

$$mathrm{mathit{B}:=:ffrac{mathit{phi }}{mathit{a}};:mathit{I:=:ffrac{I_{a}}{A}};mathit{a:=:ffrac{mathrm{2}pi rl}{P}}}$$

其中，$phi$为每极磁通，$mathit{I_{a}}$为电枢电流，l为每根电枢导体的有效长度，A为并联路径数，P为极数。然后，

$$mathrm{mathit{ au _{a}}:=:ffrac{mathit{Zphi I_{a}}P}{mathrm{2}pi A}}$$

由于对于给定的直流电动机，Z、P和A是固定的。

$$mathrm{ 因此 mathit{ au _{a}}propto mathit{phi I_{a}}}$$

因此，直流电动机的扭矩与每极磁通和电枢电流成正比。