磁场中存储的能量
在上一章中,我们讨论了在机电能量转换装置中,电气系统和机械系统之间存在耦合介质。在大多数实际装置中,磁场被用作耦合介质。因此,机电能量转换装置包括电磁系统。因此,耦合介质中存储的能量以磁场的形式存在。我们可以计算机电能量转换系统磁场中存储的能量,如下所述。
考虑一个线圈,该线圈有N圈导线缠绕在磁芯上,如图 1 所示。该线圈由 v 伏电压源供电。
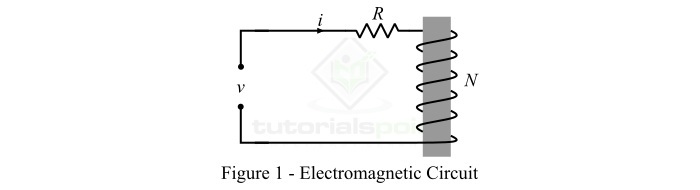
通过应用 KVL,施加到线圈的电压为,
$$mathrm{mathit{V:=:e:+:iR}cdot cdot cdot (1)}$$
其中,
e 是由于电磁感应在线圈中产生的感应 EMF。
R 是线圈电路的电阻。
$mathit{i}$ 是流过线圈的电流线圈。
电磁系统的瞬时功率输入由以下公式给出:
$$mathrm{mathit{p}:=:mathit{Vi:=:ileft ( e+iR ight )}}$$
$$mathrm{Rightarrow mathit{p}:=:mathit{ie+ i^{mathrm{2}}}mathit{R}cdot cdot cdot (2)}$$
现在,让直流电压在时间 t = 0 和 t = t1 秒结束时施加到电路,电路中的电流达到 I 安培的值。然后,在此时间间隔内,系统的能量输入为,
$$mathrm{mathit{W}_{in}:=:int_{0}^{t_{mathrm{1}}}:mathit{p:dt}}$$
$$mathrm{Rightarrow mathit{W}_{in}:=:int_{0}^{t_{mathrm{1}}}:mathit{ie:dt}:+:int_{0}^{t_{mathrm{1}}}mathit{i^{mathrm{2}}R:dt}cdot cdot cdot (3)}$$
从公式 3 可以看出,总输入能量由两部分组成 −
第一部分是储存在磁场中的能量。
第二部分是由于线圈的电阻而耗散的能量。
因此,系统磁场中储存的能量为,
$$mathrm{mathit{W}_{mathit{f}}:=:int_{0}^{t_{mathrm{1}}}:mathit{ie:dt}:cdot cdot cdot (4)}$$
根据法拉第电磁感应定律,我们有,
$$mathrm{mathit{e}:=:ffrac{mathit{dpsi }}{mathit{dt}}:=:ffrac{mathit{d}}{mathit{dt}}left ( mathit{Nphi } ight ):=:mathit{N}ffrac{mathit{dphi }}{mathit{dt}}cdot cdot cdot (5)}$$
其中,$psi$ 为磁通链,等于 $mathit{psi :=:Nphi }$。
$$mathrm{ 因此 mathit{W_{f}}:=:int_{0}^{mathit{t_{mathrm{1}}}}ffrac{mathit{dpsi }}{mathit{dt}}mathit{i:dt}}$$
$$mathrm{Rightarrow mathit{W_{f}}:=:int_{0}^{psi_{mathrm{1}}}mathit{i:dpsi }cdot cdot cdot (6)}$$
因此,方程 (6) 表明,磁场中存储的能量等于电磁系统的 ($psi -i$) 曲线(即磁化曲线)与磁通链 ($psi$) 轴之间的面积,如图 2 所示。
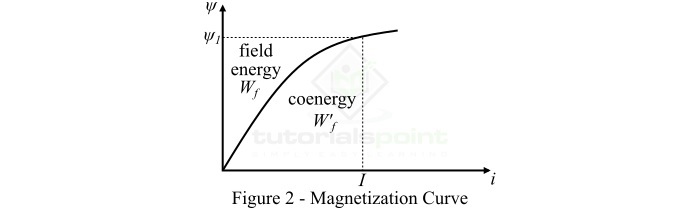
对于线性电磁系统,磁场中存储的能量为通过,
$$mathrm{mathit{W_{f}}:=:int_{0}^{mathit{psi _{mathrm{1}}}}mathit{idpsi }:=:int_{0}^{psi_{mathrm{1}} }ffrac{psi }{mathit{L}}mathit{dpsi }}$$
其中,$psi:=:mathit{Nphi }:=:mathit{Li}$ 且 L 为线圈的自感。
$$mathrm{ 因此 mathit{W_{f}}:=:ffrac{psi ^{mathrm{2}}}{2mathit{L}}:=:ffrac{1}{2}mathit{Li^{mathrm{2}}}cdot cdot cdot (7)}$$
余能的概念
余能是一个虚构的概念,用于推导电磁系统中产生的扭矩的表达式。因此,余能在该系统中没有物理意义。
基本上,余能是 $psi -i$ 曲线与电流轴之间的面积,用 $mathit{W_{f}^{'}}$ 表示,如上图 2 所示。
从数学上讲,余能由以下公式给出:
$$mathrm{mathit{W_{f}^{'}}:=:int_{0}^{i}psi mathit{di}:=:int_{0}^{i}mathit{Li:di}}$$
$$mathrm{Rightarrow mathit{W_{f}^{'}}:=:ffrac{1}{2}mathit{Li^{mathrm{2}}}cdot cdot cdot (8)}$$
从方程 (7) 和 (8) 可知,对于线性磁系统,磁场中储存的能量与余能相等。