三相的输出功率交流发电机
考虑一个具有圆柱形转子并以滞后功率因数运行的三相交流发电机。
假设,
E = 每相感应 EMF
V = 每相端电压
Ia = 每相电枢电流
cos$phi$ = 负载功率因数(滞后)
$delta$ = 功率角(E 和 V 之间的角度)
因此,三相交流发电机的输出功率为by,
$$mathrm{mathit{P_{0}}:=:3mathit{VI_{a}cosphi }cdot cdot cdot (1)}$$
三相交流发电机的近似输出功率
在三相交流发电机中,电枢电路的电阻 $R_{a}$ 与机器的同步电抗 $X_{s}$ 相比非常小。因此,我们可以忽略电枢电阻 ($R_{a}$),之后我们得到如图 1 所示的交流发电机的近似等效电路。电路的相量图也显示在图 1 中。
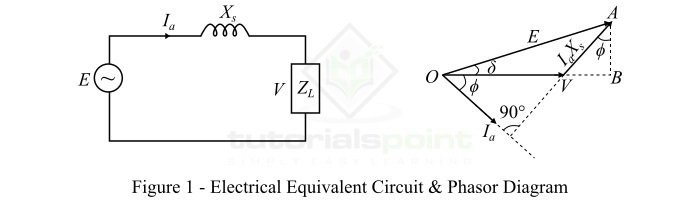
从相量图中,我们得到,
$$mathrm{mathit{AB}:=:mathit{I_{a}X_{s}cosphi }:=:mathit{E}:mathrm{sindelta }}$$
$$mathrm{Rightarrow mathit{I_{a}cosphi }:=:ffrac{mathit{E:mathrm{sindelta }}}{mathit{X_{s}}}cdot cdot cdot (2)}$$
现在,从公式 (1) 和 (2),我们得到,
$$mathrm{mathit{P_{0}}:=:ffrac{3mathit{EV:mathrm{sindelta }}}{mathit{X_{s}}}cdot cdot cdot (3)}$$
公式 3 中的表达式给出了三相交流发电机的近似输出功率。
当交流发电机以恒定的速度和恒定的励磁电流运行时,Xs 和 E 都是恒定的,因此端电压 V 也是恒定的。因此,从公式 3 中,我们可以观察到,
$$mathrm{mathit{P_{0}}propto :mathrm{sindelta }}$$
我们知道,当 $delta$ = 90° 时,
$$mathrm{mathrm{sin:90^{circ}}:=:1}$$
因此,交流发电机在 $$ =90° 时提供最大功率,其公式为,
$$mathrm{mathit{P_{max}}:=:ffrac{3mathit{EV}}{mathit{X_{s}}}}cdot cdot cdot (4)$$
公式 4 给出的最大功率称为 发电机的静态稳定极限交流发电机。
数值示例
一台三相、11 kV、3 MVA 星型连接交流发电机,每相同步电抗为 10 $Omega$。其激励使得产生的线 EMF 为 15 kV。当交流发电机连接到无限大母线时。计算在给定激励下,当忽略电枢电阻时交流发电机的最大输出功率。
解决方案
给定数据,
$$mathrm{mathrm{线电压,}mathit{V_{L}}:=:11:kV:=:11000:V}$$
$$mathrm{因此:mathrm{每相端电压}mathit{V}:=:ffrac{11000}{sqrt{3}}:=:6350.85:V}$$
$$mathrm{mathrm{产生的线电动势}:=:15:kV:=:15000:V}$$
$$mathrm{ 因此:mathrm{每相产生的电动势}mathit{E}:=:ffrac{15000}{sqrt{3}}:=:8660.25:V}$$
$$mathrm{mathrm{每相同步电抗相,}:mathit{X_{s}}:=:10:Omega }$$
因此,交流发电机的最大功率输出为,
$$mathrm{mathit{P_{max}}:=:ffrac{3mathit{EV}}{mathit{X_{s}}}:=:ffrac{3 imes 8660.25 imes 6350.85}{10}}$$
$$mathrm{ 因此 mathit{P_{max}}:=:16499 imes 10^{3}W:=:16499:mathrm{kW}}$$