同步电动机产生的功率
在本章中,我们将推导三相同步电动机产生的机械功率 (Pm) 的表达式。这里,我们将忽略同步电动机的电枢电阻Ra。然后,电枢铜损将为零,因此电机产生的机械功率等于电机的输入功率(Pin),即
$$mathrm{mathit{P_{m}}:=:mathit{P_{in}}}$$
现在,考虑一个欠励(即Eb<V)三相同步电机,其电枢电阻为零(即Ra = 0),并且正在驱动机械负载。
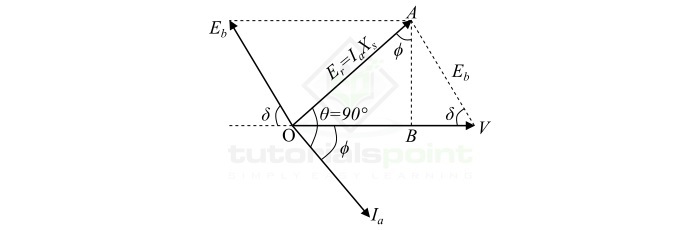
图中显示了该同步电机一相的相量图。因为电机励磁不足,所以它将以滞后功率因数运行,比如 (cos $phi$)。从相量图可清楚看出,$mathit{E_{r}}:=:I_{a}X_{s}$,每相电枢电流 $I_{a}$ 滞后于合成 EMF $mathit{E_{r}}$ 90°。
因此,电机每相的输入功率由下式给出:
$$mathrm{mathit{P_{in}}:=mathit{VI_{a}}:cos:phi :cdot cdot cdot (1)}$$
由于 $mathit{P_{m}}$ 等于 $mathit{P_{in}}$,因此:
$$mathrm{mathit{P_{m}}:=mathit{VI_{a}}:cos:phi :cdot cdot cdot (2)}$$
从相量图可知,
$$mathrm{mathit{AB}:=mathit{I_{a}X_{s}}:cos:phi :=:mathit{E}_{mathit{b}}:sin:delta}$$
$$mathrm{ 因此 mathit{I_{a}:cosphi :=:ffrac{E_{b}:sindelta }{mathit{X_{s}}}}:cdot cdot cdot (3)}$$
利用方程 (2) 和 (3),我们获得,
$$mathit{P_{m}:=:ffrac{mathit{VE_{b}}sindelta }{X_{s}}}cdot cdot cdot (4)$$
这是同步电动机每相产生的机械功率 (Pm) 的表达式。
对于电动机的三相,产生的机械功率由以下公式给出:
$$mathit{P_{m}:=:ffrac{3mathit{VE_{b}}sindelta }{X_{s}}}cdot cdot cdot (5)$$
此外,从方程 (4) 和 (5) 可清楚看出,当电功率角 ($delta$= 90°) 时,产生的机械功率最大。因此,
对于每相,
$$mathit{P_{max}:=:ffrac{mathit{VE_{b}}}{X_{s}}}cdot cdot cdot (6)$$
对于三相,
$$mathit{P_{max}:=:ffrac{mathit{3VE_{b}}}{X_{s}}}cdot cdot cdot (7)$$
要点
关于三相同步电动机产生的机械功率,以下要点值得注意 −
同步电机产生的机械功率随功率角 ($delta$) 的增加而增加,反之亦然。
如果功率角 ($delta$) 为零,则同步电机无法产生机械功率。
当同步电机的励磁减小到零,即 ($E_{b}$ = 0) 时,电机产生的机械功率也为零,即电机将停止。
数值示例
三相、4000 kW、3.3 kV、200 RPM、50 Hz 同步电机的每相同步电抗为 1.5 $Omega$。满载时,功率角为 22° 电角度。如果每相产生的反电动势为 1.7 kV,计算产生的机械功率。产生的最大机械功率是多少?
解决方案
给定数据,
每相电压,$mathit{V}:=:ffrac{3.3}{sqrt{3}}:=:1.9:kV$
每相反电动势,$mathit{E_{b}}:=:1.7:kV$
同步电抗,$X_{s}:=:1.5Omega $
功率角,$delta :=:22^{^{circ}}$
因此,电机产生的机械功率是,
$$mathrm{mathit{P_{m}}:=:ffrac{3:mathit{VE_{b}:sindelta} }{mathit{X_{s}}}:=:ffrac{3 imes 1.9 imes 1.7 imes mathrm{sin}:22^{circ}}{1.5}}$$
$$mathit{ 因此 P_{m}}:=:2.42 imes 10^{6}:W:=:2.42:MW$$
当 ($delta$ =90°) 时,产生的机械功率最大,
$$mathit{P_{max}}:=:ffrac{3mathit{VE_{b}}}{X_{s}}:=:ffrac{3 imes 1.9 imes 1.7}{1.5}$$
$$mathit{ 因此 P_{max}}:=:6.46:mathrm{MW}$$