变压器的 EMF 方程

对于电力变压器，EMF 方程 是一个数学表达式，用于查找变压器绕组中感应 EMF 的大小。

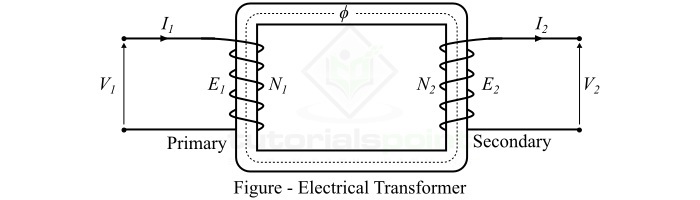
考虑如图所示的变压器。假设 N₁ 和 N₂ 是初级和次级绕组的匝数。当我们将频率为 f 的交流电压 V₁ 施加到初级绕组时，铁芯中的初级绕组会产生交变磁通量 $phi$。

如果我们假设正弦交流电压，则磁通量可由下式给出：

$$mathrm{mathit{phi }:=:phi _{m}:mathrm{sin}:mathit{omega t}:cdot cdot cdot (1)}$$

现在，根据电磁感应原理，初级绕组中感应出的 EMF e₁ 的瞬时值如下：通过，

$$mathrm{mathit{e_{mathrm{1}}}:=:mathit{-N_{mathrm{1}}}ffrac{mathit{dphi }}{mathit{dt}}}$$

$$mathrm{Rightarrow mathit{e_{mathrm{1}}}:=:mathit{-N_{mathrm{1}}}ffrac{mathit{d}}{mathit{dt}}left ( phi _{m}: mathrm{sin}:mathit{omega t} ight )}$$

$$mathrm{Rightarrow mathit{e_{mathrm{1}}}:=:mathit{-N_{mathrm{1}}}:mathit{omega phi :cos:omega t}}$$

$$mathrm{Rightarrow mathit{e_{mathrm{1}}}:=:-mathrm{2}mathit{pi fN_{mathrm{1}}}:mathit{phi_{m} :cos:omega t}}$$

其中，

$$mathrm{mathit{omega :=:mathrm{2}pi f}}$$

$$mathrm{因为 -mathit{cos:omega t}:=:mathrm{sin}left ( mathit{omega t-mathrm{90^{circ}}} ight )}$$

因此，

$$mathrm{mathit{e_{mathrm{1}}}:=:mathrm{2}mathit{phi fN_{mathrm{1}}}:mathit{phi_{m}:mathrm{sin}left ( mathit{omega t-mathrm{90^{circ}}} ight )}}:cdot cdot cdot (2)$$

等式 (2) 可以写成因为，

$$mathrm{mathit{e_{mathrm{1}}}:=:mathit{E_{m_{mathrm{1}}}}mathrm{sin}left ( mathit{omega t-mathrm{90^{circ}}} ight ):cdot cdot cdot (3)}$$

其中，$mathit{E_{m_{mathrm{1}}}}$ 为感应 EMF $mathit{e_{mathrm{1}}}$ 的最大值。

$$mathrm{mathit{E_{mathrm{m1}}}:=:mathrm{2}mathit{pi fN_{mathrm{1}}}:mathit{phi_{m}}}$$

现在，对于正弦电源，初级绕组 EMF 的 RMS 值 $mathit{E_{mathrm{1}}}$ 由下式给出：

$$mathrm{mathit{E_{mathrm{1}}}:=:ffrac{mathit{E_{mmathrm{1}}}}{sqrt{2}}:=:ffrac{2mathit{pi fN_{mathrm{1}}}phi_{m}}{sqrt{2}}}$$

$$mathrm{ 因此mathit{E_{mathrm{1}}}:=:4.44:mathit{fphi _{m}N_{mathrm{1}}}:cdot cdot cdot (4)}$$

类似地，次级绕组 EMF 的 RMS 值 E₂ 为，

$$mathrm{mathit{E_{mathrm{2}}}:=:4.44:mathit{fphi _{m}N_{mathrm{2}}}:cdot cdot cdot (5)}$$

一般而言，

$$mathrm{mathit{E}:=:4.44:mathit{fphi _{m}N}:cdot cdot cdot (6)}$$

等式 (6) 被称为 EMF 等式变压器。

对于给定的变压器，如果我们将 EMF 方程除以电源频率，我们得到，

$$mathrm{ffrac{mathit{E}}{mathit{f}}:=:4.44:phi _{m}mathit{N}:=:mathrm{Constant}}$$

这意味着每单位频率的感应 EMF 是恒定的，但它在给定变压器的初级和次级侧并不相同。

此外，从方程 (4) 和 (5)，我们有，

$$mathrm{ffrac{mathit{E_{mathrm{1}}}}{mathit{E_{mathrm{2}}}}:=:ffrac{mathit{N_{mathrm{1}}}}{mathit{N_{mathrm{2}}}}:或:ffrac{mathit{E_{mathrm{1}}}}{mathit{N_{mathrm{1}}}}:=:ffrac{mathit{E_{mathrm{2}}}}{mathit{N_{mathrm{2}}}}}$$

因此，在变压器中，初级绕组每匝感应电动势等于次级绕组每匝感应电动势。

数值示例

单相3300/240 V、50 Hz 变压器的铁芯中最大磁通量为 0.0315 Wb。计算初级和次级绕组的匝数。

解决方案

给定数据，

$$mathrm{mathit{E_{mathrm{1}}:=:mathrm{3300}:mathrm{V}:mathrm{and}:mathit{E_{mathrm{2}}:=:mathrm{240}:V}}}$$

$$mathrm{mathit{f}:=:50:Hz;:phi _{m}:=:0.0315:Wb}$$

变压器的 EMF 方程为，

$$mathrm{mathit{E}:=:4.44:mathit{fphi _{m}N}}$$

因此，对于初级绕组，

$$mathrm{mathit{N_{mathrm{1}}}:=:ffrac{mathit{E_{mathrm{1}}}}{4.44:mathit{fphi _{m}}}:=:ffrac{3300}{4.44 imes 50 imes 0.0315}}$$

$$mathrm{mathit{N_{mathrm{1}}}:=:471.9:=:472}$$

同样，对于次级绕组，

$$mathrm{mathit{N_{mathrm{2}}}:=:ffrac{mathit{E_{mathrm{2}}}}{4.44:mathit{fphi _{m}}}:=:ffrac{240}{4.44 imes 50 imes 0.0315}}$$

$$mathrm{mathit{N_{mathrm{2}}}:=:34.32:=:35}$$

绕组不可能有部分匝数。因此，匝数应为整数。