最小值和最大值

局部最小值或最小化

如果 $fleft ( \bar{x} ight )leq fleft ( x ight ),fforall x in N_varepsilon left ( \bar{x} ight )$，其中 $N_varepsilon left ( \bar{x} ight )$ 表示 $\bar{x}$ 的邻域，即 $N_varepsilon left ( \bar{x} ight )$ 表示 $left |，则 $\bar{x}in :S$ 被称为函数 $f$ 的局部最小值x-\bar{x} ight |< varepsilon$

局部最大值或最大化器

如果 $fleft ( \bar{x} ight )geq fleft ( x ight ), fforall x in N_varepsilon left ( \bar{x} ight )$，则称 $\bar{x}in :S$ 为函数 $f$ 的局部最大值，其中 $N_varepsilon left ( \bar{x} ight )$ 表示 $\bar{x}$ 的邻域，即 $N_varepsilon left ( \bar{x} ight )$ 表示 $left | x-\bar{x} ight |< varepsilon$

全局最小值

如果 $fleft ( \bar{x} ight )leq fleft ( x ight ), fforall x in S$，则 $\bar{x}in :S$ 被称为函数 $f$ 的全局最小值

全局最大值

如果 $fleft ( \bar{x} ight )geq fleft ( x ight ), fforall x in S$，则 $\bar{x}in :S$ 被称为函数 $f$ 的全局最大值

示例

步骤 1 −找到 $fleft ( \bar{x} ight )=left | x^2-4 ight |$ 的局部最小值和最大值

解决方案 −

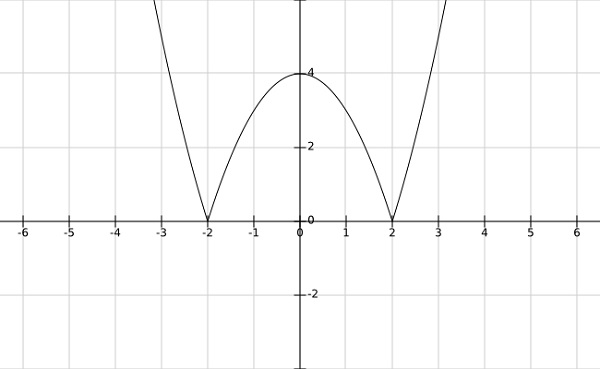
从上述函数的图中可以清楚地看出，局部最小值出现在 $x= pm 2$ 处，局部最大值出现在 $x = 0$ 处

步骤 2 − 找到函数 $fleft (x ight )=left | 的全局最小值4x^3-3x^2+7 ight |$

解决方案 −

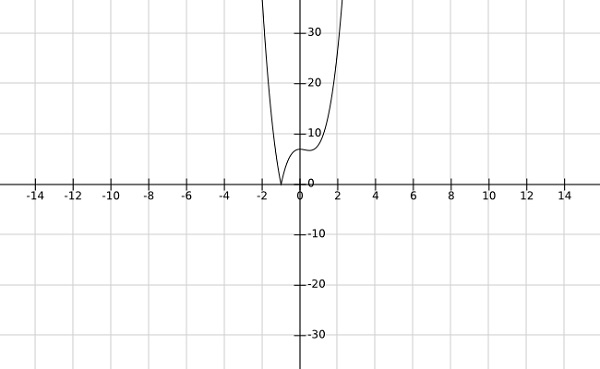
从上述函数的图中可以清楚地看出，全局最小值出现在 $x=-1$ 处。